Endless forms most beautiful*
‘A molecular endless (74) knot’ David A. Leigh, Jonathan J. Danon, Stephen D. P. Fielden, Jean-François Lemonnier, George F. S. Whitehead and Steffen L. Woltering, Nat Chem, 13, 117-122 (2021). Full Article.
.png)



[A traditional Chinese blue calico tapestry featuring a molecular endless knot. Design by Profs Bailang Yu and Xi Tang and student Ziqi Su, School of Geographic Sciences, East China Normal University.]
"The ultimate aspiration..."
In 1992, less than a decade after Jean-Pierre Sauvage’s lab carried out the first metal template synthesis of a [2]catenane,1 Daryle H. Busch (who along with, independently, Neil F. Curtis2 was the first3 to recognise and exploit metal template effects in chemical synthesis) predicted4 the possibility of “molecular weaving” from “orderly entanglements” based on metal coordination complexes. A few years later, Busch & then-graduate student Tim Hubin went a step further, proposing5 a vision for woven molecular designs, including concepts such as the one shown in Figure 1. Busch and Hubin suggested that “The ultimate aspiration of chemists working on interlocked structures might be to weave molecules as if they were macroscopic threads”, concluding that “Although this goal seems distant, progress is being made”.5
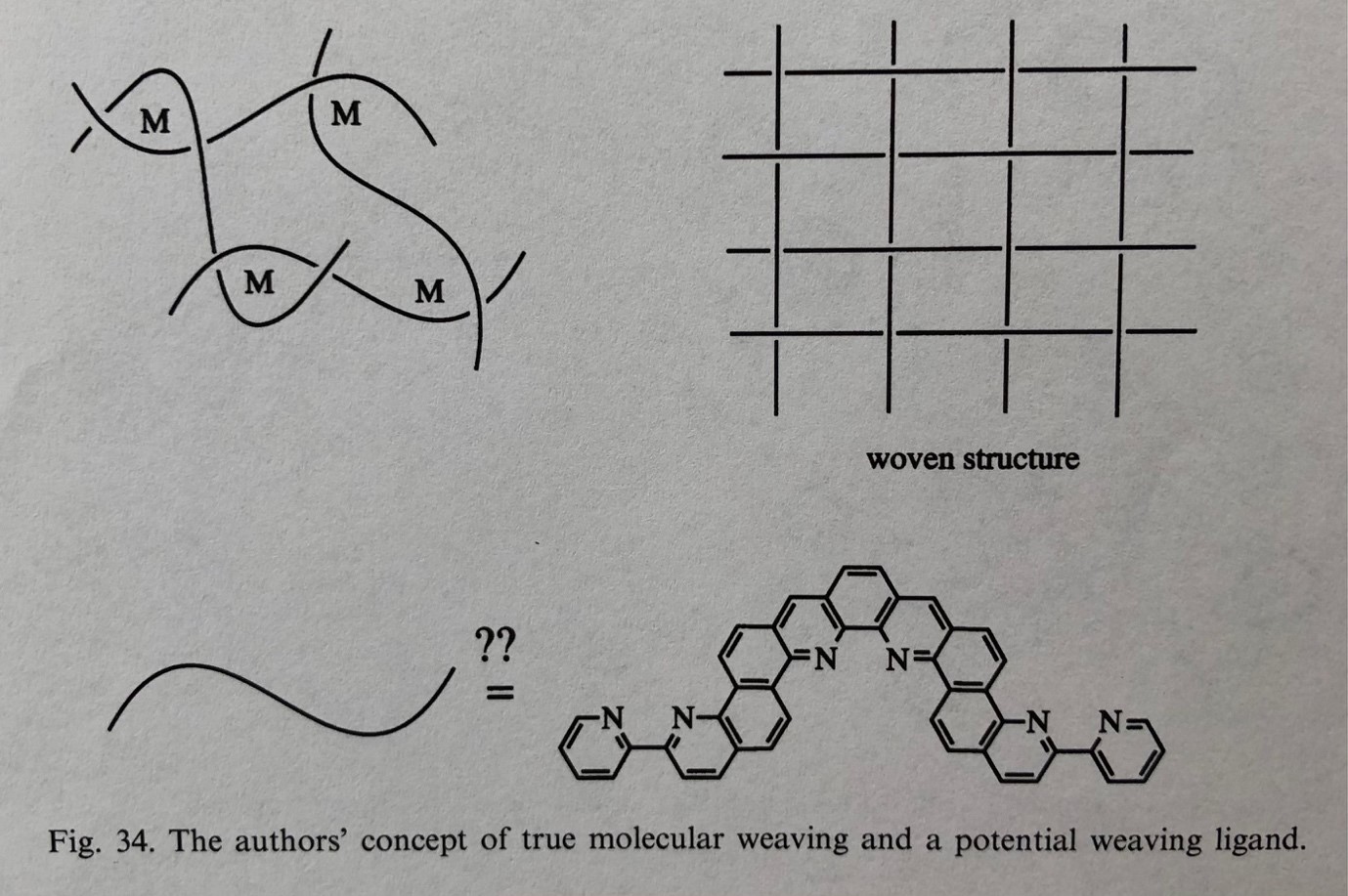
Fig. 1. Busch and Hubin’s 2000 vision of metal template “true molecular weaving”.5
Every knot is an adventure
Fast-forward a decade later, to the summer of 2010, and members of the Leigh research group were contemplating the synthesis of molecular knots. We were already well-versed in the synthesis of catenanes and rotaxanes; we had spent 15 years using hydrogen bonding to make and operate molecular machines based on interlocked architectures, and additionally had greatly expanded the ways that metal coordination geometries could be used for the template synthesis of catenanes and rotaxanes. In 2006 we had introduced active template synthesis,6 a strategy7 that fused the preferred coordination geometries of metal ions together with their propensity for catalysis to bring about the synthesis of interlocked structures using sub-stoichiometric amounts of metals. Paul McGonigal (now an Assistant Professor at the University of Durham, UK) showcased the power and versatility of the then-new synthetic strategy by using it to fold, entangle and covalently-capture a trefoil knot from a molecular strand, all in a single step.8 But in 2010 that achievement actually represented the pinnacle of molecular knot synthesis. The Sauvage lab had made a molecular trefoil knot in 1989,9 but more than 20 years later no one had been able to synthesize any knot more complicated than that. Given that mathematicians had tabulated >6 billion different prime knots with 23 or less alternating crossings,10 it was extraordinary that chemists could only make one type of knot!
However, that meant that the situation presented—and still does—a fantastic opportunity for synthetic chemistry: a truly vast region of uncharted chemical space exists (not just topology-wise but also in terms of knot chemical constitution) for which synthetic methods and strategies are unknown and virtually unexplored.
In the intervening decade we developed effective routes to several higher-order knots and links using double11 and triple12 circular helicates, while other groups pioneered coordination-directed assembly of metalloknots13 and employed solvophobic effects14. Our group have also recently explored ways to direct single-strand folding and entanglement, including controlling the stereochemistry of new crossings.15 Nevertheless, at present there is no general strategy that allows, even in principle, the synthesis of any designated molecular topology – every knot is an adventure!
Going off the grid
While we were developing the circular helicate strategy to complex knots and links, then-post-doc Jon Beves (now an Associate Professor at the University of New South Wales, Australia) came up with a brilliant complementary plan: woven grids. Jon led our team that made Solomon links using 2x2 woven grids,16 but his original sketch (on a page from a 2011 RyanAir magazine) showing how the concept could, in principle, be used to make a 74 endless knot using a 3x3 interwoven grid is shown in Figure 2, together with the first design we worked on (developed by Jon, Jean-François Ayme, Chris Campbell and Jon Danon during our annual group conference, at that time held on the shores of Loch Tay in Scotland).

Fig. 2. 2011 concept for a 74 knot based on an interwoven 3x3 grid, together with the first group ‘flowsheet’ on the project.
The concept of using a 3x3 woven grid to form a 74 knot was published in our 2013 Chem. Soc. Rev. review ‘Template synthesis of molecular knots’,17 the only issue being that molecular 3x3 woven grids were unknown! That took another seven years to solve. The key problem is that although sticks can be woven and held together only by the pressure exerted between them at the crossing points, for a woven supramolecular structure such stresses impose limitations and tolerances on metal-donor distances and geometries for internal coordination sites. Our early designs for 3x3 interwoven grids featured strong terpyridine-like coordination motifs for the difficult centre-of-the-cross position, with weaker binding TTZ units (a potential heterocyclic ligand introduced by the Steel group a few years earlier18) intended to bind labile metal ions on alternate sides of the ligand, with a structure designed to ensure the nine binding sites would all lie within the same plane. Although these early designs did not themselves form 3x3 interwoven grids, they provided the basis for later successful designs. The later stages of the evolution of the ligand design are outlined below.
Gridlocked
One of the ligand strands we investigated is shown in Fig. 3. It’s a tritopic ligand, with an additional TTZ moiety and pyridine core intended to provide the key central coordination site. Treatment of the ligand with Zn(OTf)2 in apolar solvents showed a complicated product mixture with some evidence (by mass spectrometry and 1H NMR) for coordination of two strands through a corner join.
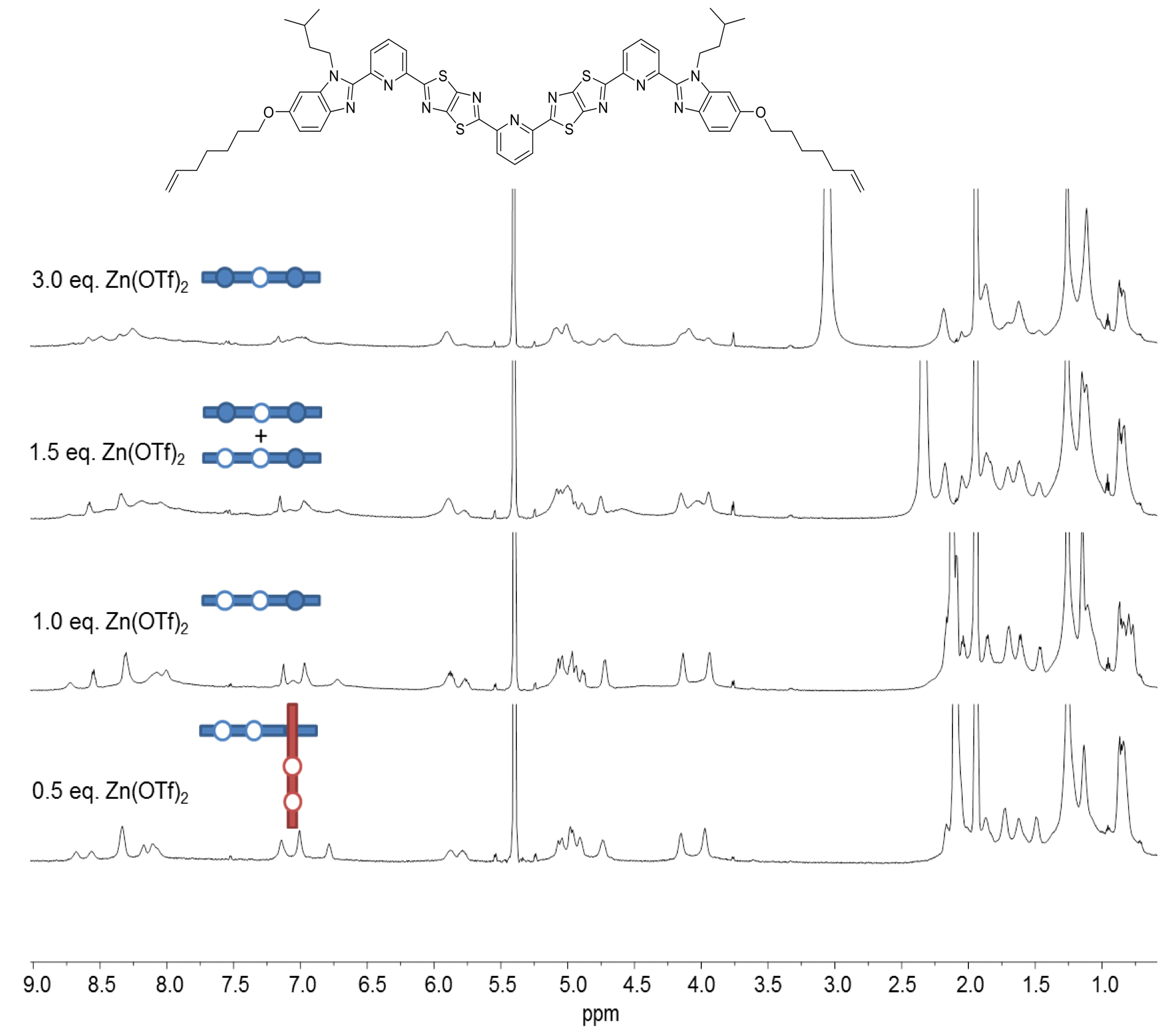
Fig. 3. 1H NMR (600 MHz, 298 K) spectra of titration of a ligand strand with Zn(OTf)2 in a mixture of CD3CN/CD2Cl2. White circles indicate empty coordination sites; coloured circles occupied ones.
As the binding between zinc(II) and the central site of the ligand appeared to be insufficient in the design, electron-donating methoxy groups were added to the pyridine groups (Fig. 4). The new ligand also formed corner complexes with Zn(OTf)2. There was also mass spectrometric evidence for assembly of four strands into a square, but still no sign of the elusive six-strand interwoven grid.
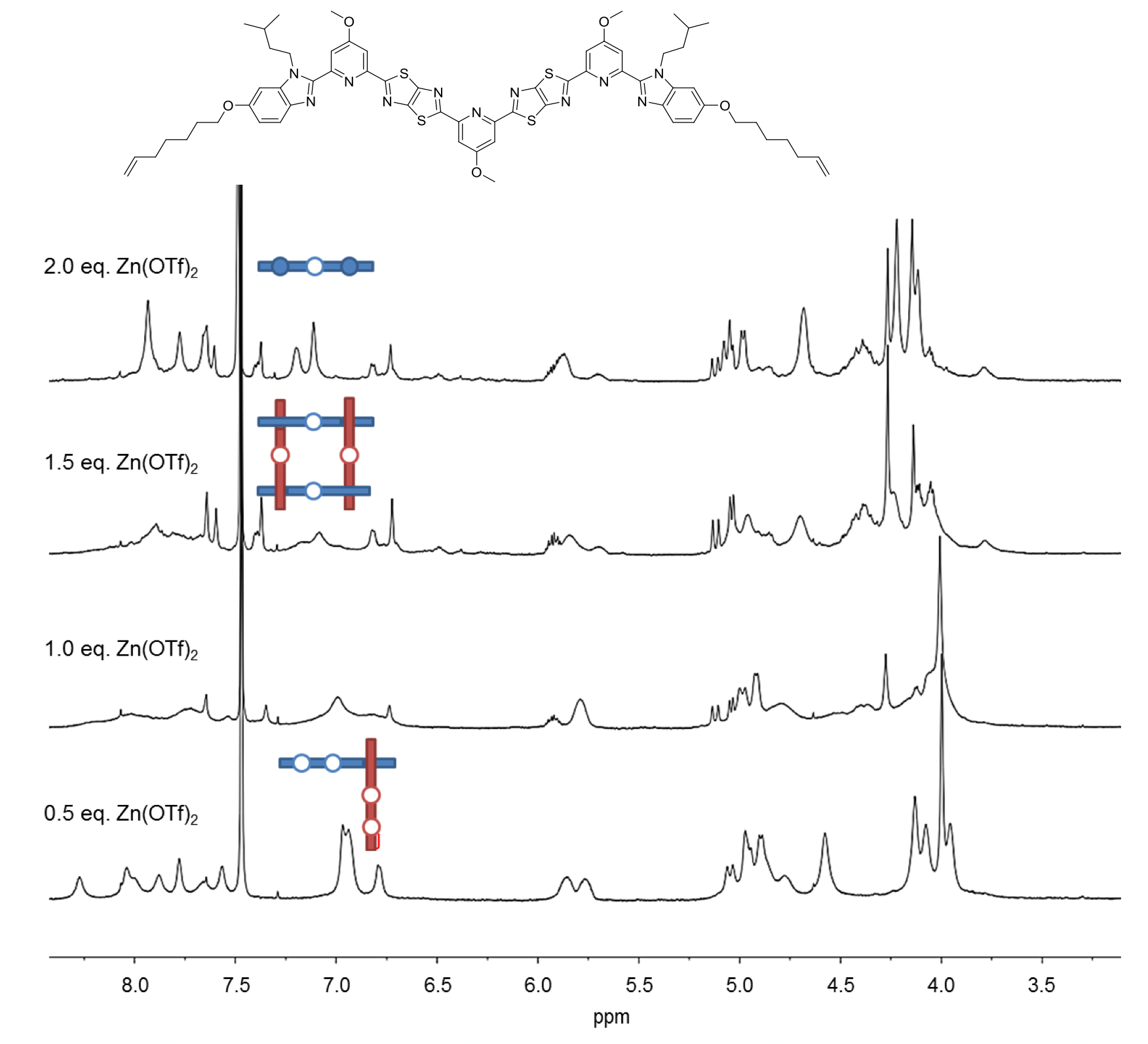
Fig. 4. 1H NMR (600 MHz, 298 K) spectra of titration of second ligand strand design with Zn(OTf)2 in a mixture of CD3CN/CD2Cl2.
The coordinating ability of the central pyridine unit was further enhanced by replacing the methoxy group with a dimethylamino one (Fig. 5), with the outer pyridines reverting to being unsubstituted at the 4-position to maximise the difference between the outer and difficult internal sites. When 1.5 equiv. of Zn(OTf)2 was added to this ligand, the theoretical stoichiometry required for nine zinc cations to bind to six ligands, a complex mixture of species was observed but still with no sign of interwoven grid formation (Fig. 5).
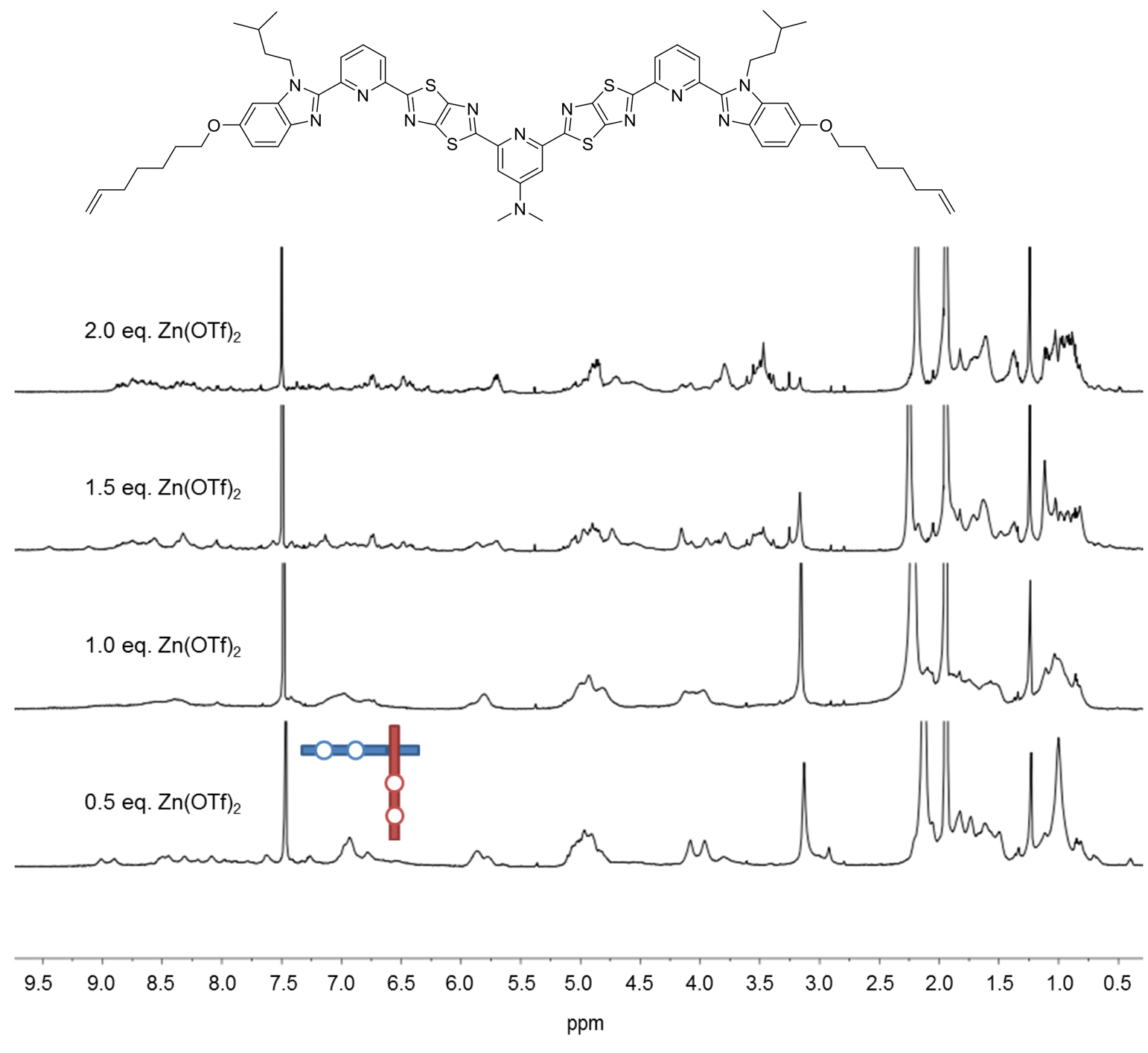
Fig. 5. 1H NMR (600 MHz, 298 K) spectra of titration of third ligand strand design with Zn(OTf)2 in a mixture of CD3CN/CD2Cl2.
At this point, postdoc Jean-François Lemonnier recalled that the X-ray crystal structure of the Solomon link constructed from the smaller 2x2 grid was of the BF4- salt, and featured a well-ordered BF4- anion in the central ‘square’ of the 2x2 interwoven grid.16 He switched from using Zn(OTf)2 to coordinate the ligand strands to Zn(BF4)2 with immediate, quite extraordinary, results. Within 5 minutes of mixing the ligands with Zn(BF4)2 in the required 3:2 stoichiometry (i.e. 9 metals to 6 ligands), the interwoven 3x3 grid assembled quantitatively (Fig. 6).
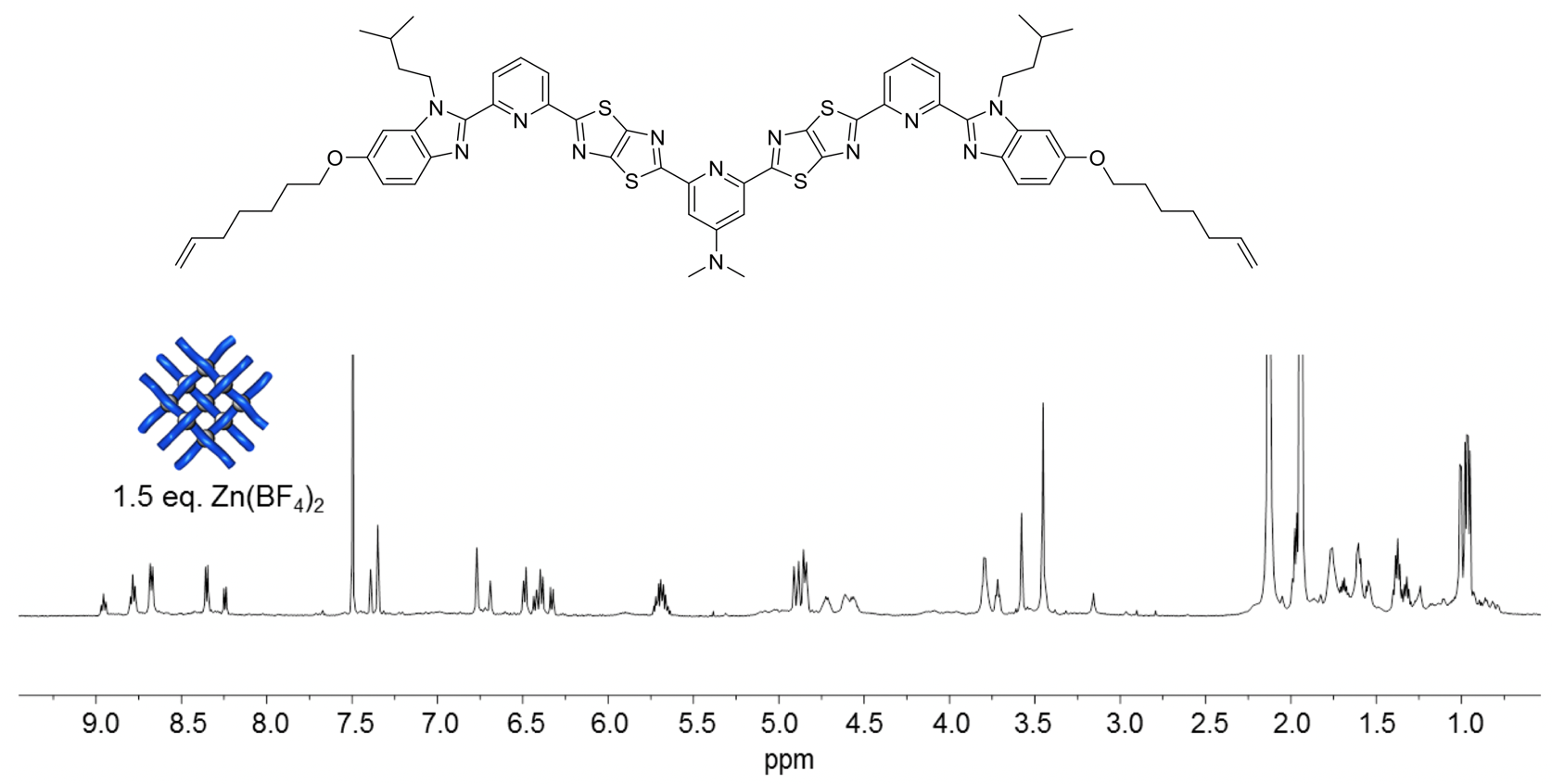
Fig. 6. 1H NMR (600 MHz, 298 K) spectra of titration of third ligand strand design with Zn(BF4)2 in a mixture of CD3CN/CD2Cl2.
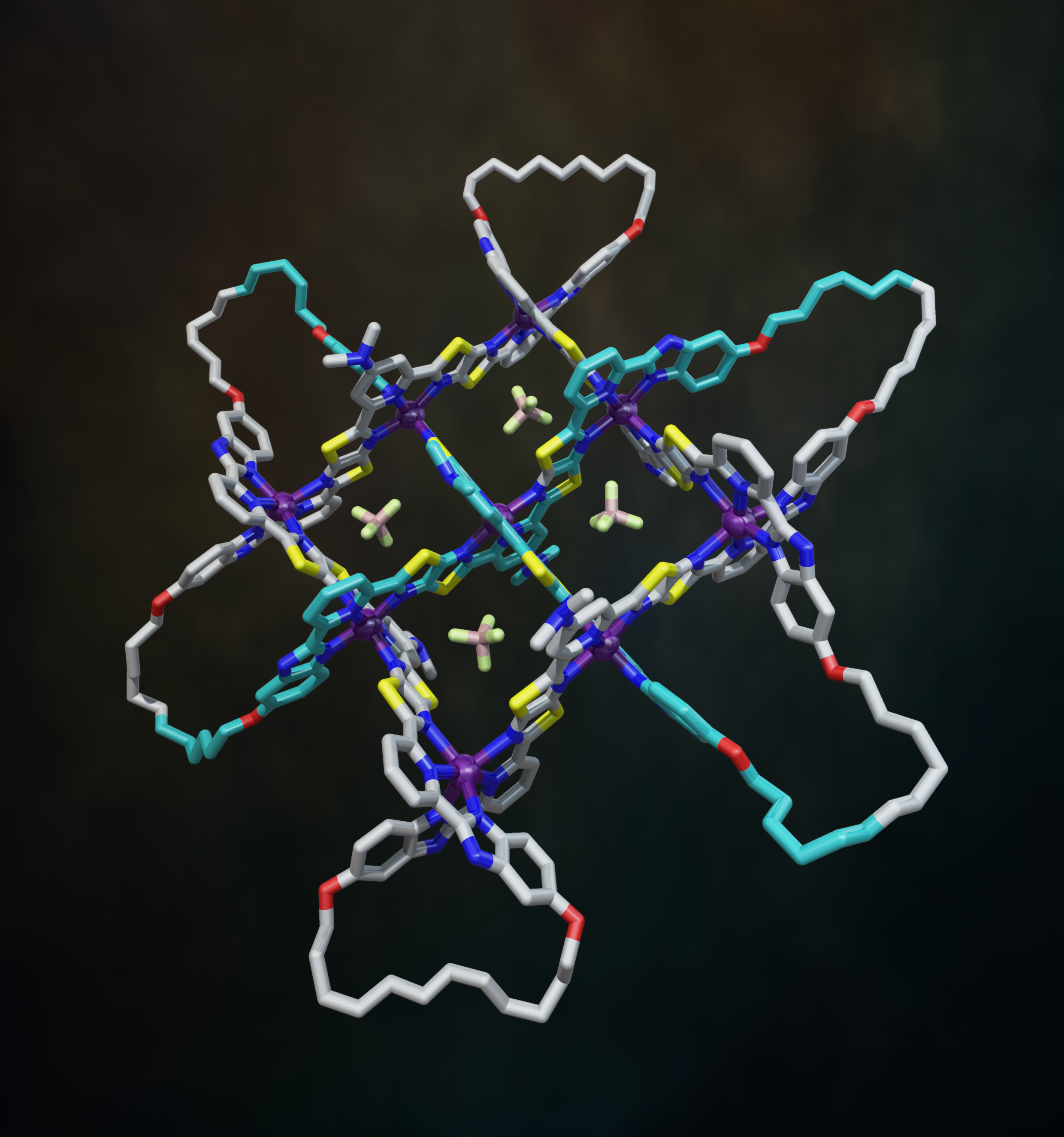
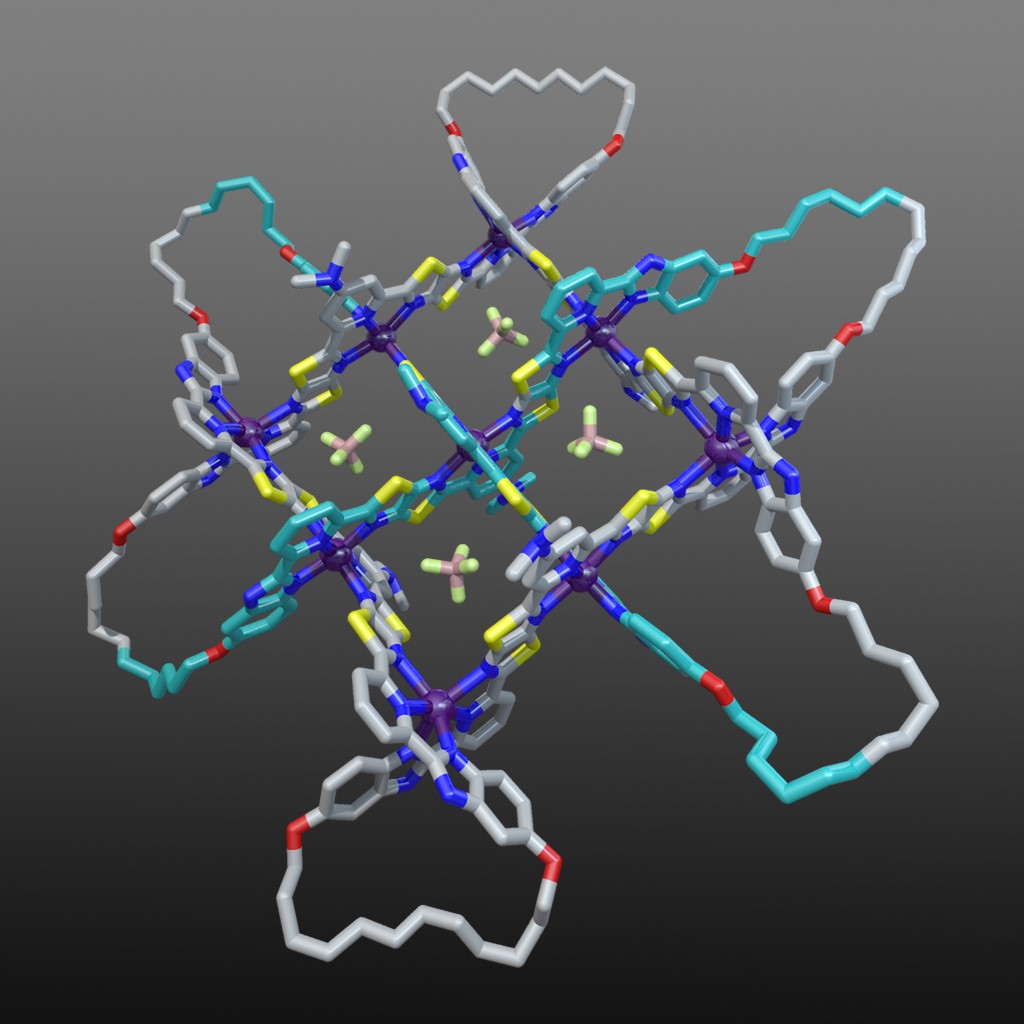
The X-ray crystal structure of the interwoven 3x3 grid confirmed its architecture and ring-closing olefin metathesis subsequently afforded the 258-atom-long, closed loop, 74 endless knot (along with a simple macrocycle and a Solomon link).19 Figure 7 shows the structure of the 74 knot coordination complex (with 6 x Fe(BF4)2) based on the X-ray structure of the 3x3 interwoven grid with modelled cyclized end groups. The X-ray structure also showed the key role played by the BF4- anions: four of them bind in the square cavities formed between the criss-crossed coordinated ligand strands (Fig. 7). The binding energy provided by those interactions are sufficient to stabilize the entire structure to the extent that the formation of the woven grid becomes favourable.

Fig. 7. Molecular 74 knot coordination complex (with 6 x Fe(BF4)2) based on the X-ray structure of the 3x3 interwoven grid with modelled cyclized end groups. Video credit: Alberto Valero.
An endless challenge
Despite a decade of design it was ultimately an unanticipated BF4- template effect, tried only because of the recollection and recognition of interactions present in an X-ray crystal structure of a related Solomon link, that led to the assembly of the key interwoven 3x3 grid. The story of the synthesis of this molecular knot illustrates well how cutting-edge scientific research often actually proceeds: one continually faces challenges that one doesn't know quite enough to definitely be able to solve. But once the problem is solved (by some combination of skill, observation, reasoning, screening and, occasionally, luck!) the answer provides insights that makes future challenges easier.

Fig. 8. The endless knot is a familiar feature in traditional Chinese art. This original artwork was created for David Leigh by Shanghai artist Ying Wu. Image credit: Ying Wu and Jo Richers; jorichers.com.
The endless knot is a basic motif of Celtic interlace, the smallest Chinese knot, and is one of the eight auspicious symbols (the Ashtamangala) common to many Eastern religions and philosophies, where it represents the union of wisdom and method (Figure 8). The practical significance of its preparation in molecular form is apparent from the lessons learnt from its synthesis, which opens the way for the bottom-up assembly of woven polymer chains20 and other knotted and entangled molecules and materials. Busch’s “ultimate aspiration” is coming tantalizingly within reach.
References
1. Dietrich-Buchecker, C. O., Sauvage, J.-P. & Kintzinger, J.-P. Une nouvelle famille de molecules: les metallo-catenanes. Tetrahedron Lett. 24, 5095–5098 (1983).
2. Curtis, N. F. The advent of macrocyclic chemistry. Supramol. Chem. 24, 439–447 (2012).
3. Thompson, M. C. & Busch, D. H. Reactions of coordinated ligands. IX. Utilization of the template hypothesis to synthesize macrocyclic ligands in situ. J. Am. Chem. Soc. 86, 3651–3656 (1964).
4. Busch, D. H. Structural definition of chemical templates and the prediction of new and unusual materials. J. Inclusion Phenom. Mol. Recognit. Chem. 12, 389–395 (1992).
5. Hubin, T. J. & Busch, D. H. Template routes to interlocked molecular structures and orderly molecular entanglements. Coord. Chem. Rev. 200–202, 5–52 (2000).
6. (a) Aucagne, V., Hänni, K. D., Leigh, D. A., Lusby, P. J. & Walker, D. B. Catalytic "click" rotaxanes: a substoichiometric metal-template pathway to mechanically interlocked architectures. J. Am. Chem. Soc. 128, 2186–2187 (2006). (b) Crowley, J. D., Goldup, S. M., Lee, A.-L., Leigh, D. A. & McBurney, R. T. Active metal template synthesis of rotaxanes, catenanes and molecular shuttles. Chem. Soc. Rev. 38, 1530–1541 (2009).
7. Denis, M. & Goldup, S. M. The active template approach to interlocked molecules: principles, progress and applications. Nat. Rev. 61 (2017).
8. Barran, P. E. et al. Active metal template synthesis of a molecular trefoil knot. Angew. Chem. Int. Ed. 50, 12280–12284 (2011).
9. Dietrich-Buchecker, C. O. & Sauvage, J.-P. A synthetic molecular trefoil knot. Angew. Chem. Int. Ed. Engl. 28, 189–192 (1989).
10. Fenlon, E. E. Open problems in chemical topology. Eur. J. Org. Chem. 5023-5035 (2008).
11. Ayme, J.-F. et al. A synthetic molecular pentafoil knot. Nat. Chem. 4, 15–20 (2012).
12. Danon, J. J. et al. Braiding a molecular knot with eight crossings. Science 355, 159–162 (2017).
13. Inomata, Y., Sawada, T. & Fujita, M. Metal-peptide torus knots from flexible short peptides. Chem 6, 294–303 (2020).
14. Cougnon, F. B. L., Caprice, K., Pupier, M., Bauza, A. & Frontera, A. A strategy to synthesize molecular knots and links using the hydrophobic effect. J. Am. Chem. Soc. 140, 12442–12450 (2018).
15. Leigh, D. A., et al. Tying different knots in a molecular strand. Nature 584, 562–568 (2020).
16. Beves, J. E., Danon, J. J., Leigh, D. A., Lemonnier, J.-F. & Vitorica-Yrezabal, I. J. A Solomon link through an interwoven molecular grid. Angew. Chem. Int. Ed. 54, 7555–7559 (2015).
17. Ayme, J.-F., Beves, J. E., Campbell, C. J. & Leigh, D. A. Template synthesis of molecular knots. Chem. Soc. Rev. 42, 1700–1712 (2013).
18. Slater, J. W. & Steel, P. J. Syntheses of new binucleating heterocyclic ligands. Tetrahedron Lett. 47, 6941–6943 (2006).
19. Leigh, D. A., Danon, J. J., Fielden, S. D. P., Lemonnier, J.-F., Whitehead, G. F. S. & Woltering, S. L. A molecular endless (74) knot. Nat. Chem, 13, 117-122 (2021)
20. August, D. P. et al. Self-assembly of a layered two-dimensional molecularly woven fabric. Nature, 588, 429-435 (2020).
21. Darwin, C. R. On the origin of species by means of natural selection. John Murray, London (1859).
